解答編

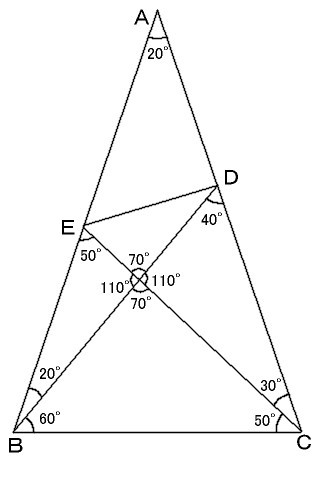
まず、問題図から、足し算引き算で求められる角度を求めます。

これは、解法A、Bいずれのやり方でも必須です。

その結果が右図です。

そして、この結果から∠BCE＝∠BEC＝50ﾟ、
つまり、三角形BCEはBC＝BEの二等辺三角形であることが分かります。

そして、この後のやり方は解法A、Bによって異なります。

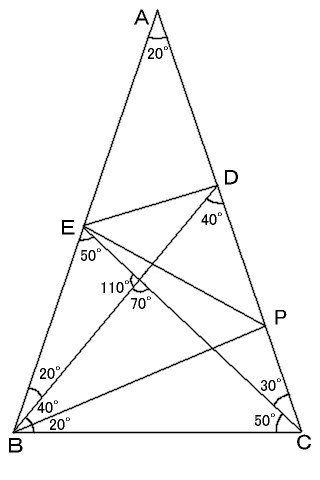
AC上に∠CBP＝20ﾟとなるような点Pをとり、PとEを結びます。（右図）
∠BPC＝180ﾟ−20ﾟ−50ﾟ−30ﾟ＝80ﾟ＝∠BCP
つまり、三角形BCPは二等辺三角形です。
よって、BC=BPです。

また∠PBD＝∠PDB＝40ﾟであり、つまり三角形BDPは二等辺三角形です。
よって、BP＝DPです。

ところで、既にBC=BEであることが分かっています。
よって、BE=BPです。
また∠EBP＝60ﾟであり、つまり三角形BEPは正三角形です。
よって、BP＝BE＝EPです。

以上のことから、DP＝EPです。
つまり、三角形DEPは二等辺三角形です。

ところで、∠DPE＝180ﾟ−80ﾟ−60ﾟ＝40ﾟです。
三角形DEPは二等辺三角形ですから、
∠PDE＝（180ﾟ−40ﾟ）÷2＝70ﾟであり、
∠BDE＝70ﾟ−40ﾟ＝30ﾟとなります。

つまり、解は30ﾟです。

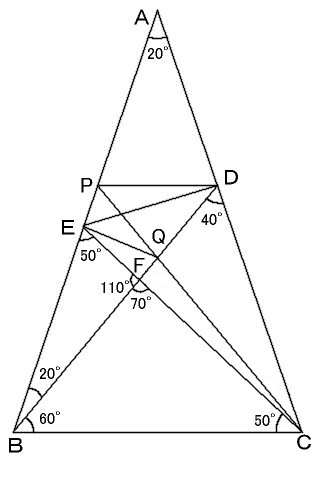
Dを通りBCに平行な直線を引き、ABとの交点をPとします。
そしてPとCを結び、BDとの交点をQとします。
そして、QとEとを結びます。（右図）

三角形PBCと三角形DCBは合同になりますので、
∠PCB＝∠DBC＝60ﾟであり、
つまり三角形BCQ、三角形DPQはそれぞれ正三角形です。
よって、BC＝BQ＝CQ、DP=PQ=QDであり、また、幾つかの角が60ﾟであることが分かります。

ところで、既にBC=BEであることが分かっています。
よってBE=BQであり、つまり三角形BQEは二等辺三角形です。
このことから∠BQE＝(180ﾟ−20ﾟ)÷2＝80ﾟであり、
∠EPQ＝180ﾟ−60ﾟ−80ﾟ＝40ﾟです。

また、∠CPB＝180ﾟ−80ﾟ−60ﾟ＝40ﾟであり、
つまり三角形EQPは二等辺三角形であり、
よってEP＝PQです。

そうすると、DP＝DQ、PE＝QE、DE＝DEとなり、
三角形DPEとDQEは合同であることが分かります。
つまり∠EDP＝EDQであり、
∠BDE＝60ﾟ÷2＝30ﾟとなります。

つまり、解は30ﾟです。